理解卡尔曼滤波

卡尔曼滤波被广泛的应用于运动估计中，在飞行器中多有应用，区别于普通滤波如低通滤波，卡尔曼滤波具有不延时的优点，即普通的低通滤波在过滤噪声的同时也会引入信号滞后，而卡尔曼滤波则可以实时估计对象状态，不产生滞后。与普通滤波不同，卡尔曼滤波基于对象的数学模型进行设计。

关于卡尔曼滤波的介绍参考

https://zh.wikipedia.org/wiki/卡尔曼滤波

或者英文网站

https://en.wikipedia.org/wiki/Kalman_filter

如上，除了对象数学模型，卡尔曼滤波包含七个公式，较为复杂，不容易理解，这也是大部分考虑采用卡尔曼滤波算法的开发者的体会，这里分享一下关于卡尔曼滤波设计的思路，便于对卡尔曼滤波取得一个简单直观的理解，以便在工程项目中方便地应用卡尔曼滤波。

在已知对象模型的条件下，我们可以把卡尔曼滤波看做和被估计对象同时运行的一个系统，这个系统的模型和对象一样，输入和对象一样，输出和对象的输出作比较。在理想条件下，对象的输出和这个模拟系统的输出应该是一样的，但是因为噪声、干扰、初始估计误差等原因，模拟系统的状态变量与对象的状态变量存在误差。卡尔曼滤波的原理就是通过比较模拟系统和对象的输出，反馈到估计量中，不断修正模拟系统中的状态变量估计，从而比较精确的估计出对象模型的状态变量。类似于自动控制中的负反馈。

如上图，假设对象模型为

$\mathbf{x}_{k} = \mathbf{F}_{k} \mathbf{x}_{k-1} + \mathbf{B}_{k} \mathbf{u}_{k} + \mathbf{w}_{k}$ （1）

对象输出为

$\mathbf{z}_k = \mathbf{H}_{k} \mathbf{x}_k + \mathbf{v}_k$ （2）

其中wk和vk为系统噪声和测量噪声。

$\mathbf{w}_k \sim \mathcal{N}(0, \mathbf{Q}_k)$

$\mathbf{v}_k \sim \mathcal{N}(0, \mathbf{R}_k)$

卡尔曼滤波的估计为

$\hat{\mathbf{x}}_{k\mid k-1} = \mathbf{F}_{k}\hat{\mathbf{x}}_{k-1\mid k-1} + \mathbf{B}_{k} \mathbf{u}_{k}$ （3）

即为与对象模型等同的一个系统，其中x为模拟系统的状态变量，即对象的状态变量估计。根据卡尔曼滤波估计得到的输出（即模拟系统的输出）与实际测量输出之间的误差为

$\tilde{\mathbf{y}}_k = \mathbf{z}_k - \mathbf{H}_k\hat{\mathbf{x}}_{k\mid k-1}$ （4）

根据误差对卡尔曼滤波估计进行校正

$\hat{\mathbf{x}}_{k\mid k} = \hat{\mathbf{x}}_{k\mid k-1} + \mathbf{K}_k\tilde{\mathbf{y}}_k$ （5）

其中K为校正增益矩阵，上述三个公式即表示了卡尔曼滤波的原理。

而方程式组中的其它公式则是计算校正增益阵K使滤波效果达到最优。如下式

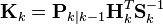$\mathbf{K}_k = \mathbf{P}_{k\mid k-1}\mathbf{H}_k^T \mathbf{S}_k^{-1}$ （6）

其中

$\mathbf{P}_{k\mid k-1} = \mathbf{F}_{k} \mathbf{P}_{k-1\mid k-1} \mathbf{F}_{k}^{\text{T}} + \mathbf{Q}_{k}$ （7）

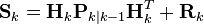$\mathbf{S}_k = \mathbf{H}_k \mathbf{P}_{k\mid k-1} \mathbf{H}_k^T + \mathbf{R}_k$ （8）

从原理上讲，K根据信号的质量来计算，包括输入的信号质量，输出的信号质量，和状态估计本身的质量，其中Q,R,P分别为输入、输出和状态变量的协方差，即

$\mathbf{P}_{k\mid k} = \mathrm{cov}(\mathbf{x}_k - \hat{\mathbf{x}}_{k\mid k})$

$\mathbf{P}_{k\mid k-1} = \mathrm{cov}(\mathbf{x}_k - \hat{\mathbf{x}}_{k\mid k-1})$

S为输出误差的协方差

$\mathbf{S}_{k} = \mathrm{cov}(\tilde{\mathbf{y}}_k)$

分别表征输入、输出、系统状态变量估计以及输出误差的信号质量，式（6）通过三个信号的协方差计算得出校正增益阵，基本上是信号质量越好（协方差越小），则在校正矩阵计算结果中所起的作用越大。状态估计协方差则由输入误差引入并根据输出误差进行校正，如下式。

$\mathbf{P}_{k|k} = (I - \mathbf{K}_k \mathbf{H}_k) \mathbf{P}_{k|k-1}$ （9）

综上所述，卡尔曼滤波是一个模拟对象系统进行估计和校正的估计方法。在实际工程应用中，建立对象的数学模型，并估计对象的输入和输出噪声方差，即可以应用卡尔曼滤波来估计对象的内部状态。

理解卡尔曼滤波

浏览过的版块